[1] 3-SUM algorithm

3-Sum algorithm은, 세 숫자의 합이 특정 조건을 만족하는 모든 경우의 수를 탐색하는 알고리즘이다. 

2-Sum 알고리즘도 있다. 애는 Linear Time에 해결할 수 있고, 이는 Hash-table을 이용하여 문제를 해결한다. 

2-Sum algorithm을 nlogn의 시간복잡도로 해결하는 방법으로 sliding-window 방식이 있는데, 3-Sum algorithm은 이 방식을 한번 더 감싼 것에 불과하다. 

 

예시 문제를 보면서 이해해보자.

 

주어진 문제에선 용액의 특성값을 나타내는 N개의 정수가 순서대로 제공된다. 그 때, 세 특성값의 합이 0에 가장 가까운 조합을 찾는것이 목적이다.

 

그냥 단순히 Brute-force로 문제를 해결하게 되면, for문을 3개 돌려서 모든 조합에 대해서 정답을 찾는 것이 되겠다. 그러나 시간복잡도가 O(n^3) 이나 된다. 시간복잡도를 한 차수를 줄이는 방법이 있다. 

 

핵심은 정렬된 상태를 이용하는 것이다.

 

우선 먼저 주어진 배열을 정렬한다(nlogn). 배열을 정렬된 상태에서, 첫번째 인덱스는 i = 0 부터 n - 1 까지 돌고 그 다음이 핵심이다. 두번째는 첫번째 다음 인덱스, 세번째는 배열의 마지막 인덱스를 지정하고, 세 값을 더했을 때 목표하는 값 보다 작으면 두번째 인덱스를 오른쪽으로 이동시키고, 크면 세번째 인덱스를 왼쪽으로 이동시키는 것이다. 

 

예제 입력을 이용하여 만든 예시를 보자. 

 

우선 이게 기본 입력상태이다. 애를 먼저 정렬해주자. 

 

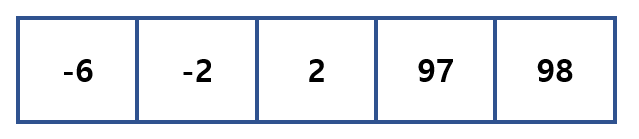
이 상태에서 Index를 각각 지정해준다.

 

목표는 0에 가까워지는 것인데, 현재 합은 90으로, 0보다 크다. 그러므로 세번째 인덱스를 왼쪽으로 옮겨준다.

 

음.. 여전히 89로 0보다 크다. 그럼 하나 더 옮기자.

아 이제 보니 합이 -6이다. 그럼 2번 인덱스를 오른쪽으로 한칸 옮겨줘야 하는데, 3번이랑 겹친다. 이렇게 되면 한 loop가 끝나게 된 것이다. 그리고 1번은 이제 오른쪽으로 한칸 이동하고, 똑같이 2번은 1번 오른쪽에, 3번은 맨 오른쪽에 배치되고 같은 로직이 반복된다.

 

핵심은, 2번과 3번 인덱스가 조합을 형성할 때 정렬된 상태를 이용하여 모든 조합을 조사하는 게 아니라, 조건에 가까운 영역만 조사를 하게 된다는 것이다. 이를 통해 시간복잡도를 한 차원 줄일 수 있다.